

Statistical models fit to compositional data are often difficult to
interpret due to the sum to one constraint on data variables.
DImodelsVis provides novel visualisations tools to aid with
the interpretation for models where the predictor space is compositional
in nature. All visualisations in the package are created using the
ggplot2 plotting framework and can be extended like every
other ggplot object.
You can install the released version of DImodelsVis from
CRAN by running:
install.packages("DImodelsVis")You can install the development version of DImodelsVis
from GitHub with:
# install.packages("devtools")
devtools::install_github("rishvish/DImodelsVis")While sometimes it is of interest to model a compositional data
response, there are times when the predictors of a response are
compositional, rather than the response itself. Diversity-Interactions
(DI) models (Kirwan et al.,
2009, Connolly et
al., 2013, Moral
et al., 2023) are a regression based modelling technique for
analysing and interpreting data from biodiversity experiments that
explore the effects of species diversity on the different outputs
(called ecosystem functions) produced by an ecosystem. Traditional
techniques for analysing diversity experiments quantify species
diversity in terms of species richness (i.e., the number of species
present in a community). The DI method builds on top of this richness
approach by taking the relative abundances of the species within in the
community into account, thus the predictors in the model are
compositional in nature. The DI approach can differentiate among
different species identities as well as between communities with same
set of species but with different relative proportions, thereby enabling
us to better capture the relationship between diversity and ecosystem
functions within an ecosystem. The DImodels
and DImodelsMulti
R packages are available to aid the user in fitting these models. The
DImodelsVis (DI models Visualisation) package is a
complimentary package for visualising and interpreting the results from
these models. However, the package is versatile and can be used with any
standard statistical model object in R where the predictor space is
compositional in nature.

The functions in the package can be categorised as functions for visualising model selection and validation or functions to aid with model interpretation. Here is a list of important visualisation functions present in the package along with a short description.
model_diagnostics: Create diagnostics
plots for a statistical model with the additional ability to overlay the
points with pie-glyphs
showing the proportions of the compositional predictor variables.model_selection: Show a visual
comparison of selection criteria of different models. Can also show the
split of an information criteria into deviance and penalty components to
visualise why a parsimonious model would be preferable over a complex
one.prediction_contributions: The
predicted response for observations is visualised as a stacked bar-chart
showing the contributions of each term in the regression model.gradient_change: The predicted
response for specific observations are shown using pie-glyphs along with
the average change in the predicted response over the richness or
evenness diversity gradients.conditional_ternary: Assuming we have
n compositional variables, fix n-3 variables
to have specific values and visualise the change in the predicted
response across the remaining three variables as a contour plot in a
ternary diagram.visualise_effects: Visualise the
effect of increasing or decreasing a predictor variable (from a set of
compositional predictor variables) on the predicted response whilst
keeping the ratio of the other n-1 compositional predictor
variables constant.simplex_path: Visualise the change in
the predicted response along a straight line between two points in the
simplex space.add_prediction: A utility function to
add prediction and associated uncertainty to data using a statistical
model object or raw model coefficients.get_equi_comms: Utility function to
create all possible combinations of equi-proportional communities at a
given level of richness from a set of n compositional variables.custom_filter: A handy wrapper around
the dplyr filter()
function enabling the user to filter rows which satisfy specific
conditions for compositional data like all equi-proportional
communities, or communities with a given value of richness without
having to make any changes to the data or adding any additional
columns.prop_to_tern_proj and
tern_to_prop_proj: Helper functions for
converting between 3-d compositional data and their 2-d
projection.ternary_data and
ternary_plot: Visualise the change in the
predicted response across a set of three compositional predictor
variables as a contour map within a ternary diagram.library(DImodels)
library(DImodelsVis)This dataset originates from a grassland biodiversity experiment
conducted in Switzerland as part of the “Agrodiversity Experiment” Kirwan et al
2014. In this study, 68 grassland plots consisting of 1 to 4 species
were established across a gradient of species diversity. The proportions
of four species were varied across the plots: there were plots with 100%
of a single species (called the monoculture of a species), and 2- and
4-species mixtures with varying proportions (e.g., (0.5, 0.5, 0, 0) and
(0.7, 0.1, 0.1, 0.1)). Nitrogen fertilizer (at 50 or 150 kg/ha/yr) and
seeding density (low or high) treatments were also manipulated across
the plots. The total annual yield per plot was recorded for the first
year after establishment. The data is available in the DImodels
R package. An analysis of the this dataset can be found in Kirwan et al 2009. For our
example we only consider the plots that received the 150 kg nitrogen
treatment. The four species proportions form our compositional
predictors while the annual yield is our continuous response.
data(Switzerland)
my_data <- Switzerland[Switzerland$nitrogen == 150, ]
head(my_data)
#> plot nitrogen density p1 p2 p3 p4 yield
#> 1 1 150 high 0.70 0.10 0.10 0.10 13.51823
#> 2 2 150 high 0.10 0.70 0.10 0.10 13.16549
#> 3 3 150 high 0.10 0.10 0.70 0.10 19.95682
#> 4 4 150 high 0.10 0.10 0.10 0.70 17.93976
#> 5 5 150 high 0.25 0.25 0.25 0.25 13.74719
#> 6 6 150 high 0.40 0.40 0.10 0.10 15.11899We fit different models with different interaction structures as described in Moral et al 2023.
mod_ID <- DI(y = "yield", prop = 4:7,
DImodel = "ID", data = my_data)
#> Fitted model: Species identity 'ID' DImodel
mod_AV <- DI(y = "yield", prop = 4:7,
DImodel = "AV", data = my_data)
#> Fitted model: Average interactions 'AV' DImodel
mod_FG <- DI(y = "yield", prop = 4:7,
DImodel = "FG", data = my_data,
FG = c("G", "G", "H", "H"))
#> Fitted model: Functional group effects 'FG' DImodel
mod_ADD <- DI(y = "yield", prop = 4:7,
DImodel = "ADD", data = my_data)
#> Fitted model: Additive species contributions to interactions 'ADD' DImodel
mod_FULL <- DI(y = "yield", prop = 4:7,
DImodel = "FULL", data = my_data)
#> Fitted model: Separate pairwise interactions 'FULL' DImodelWe can visualise model selection by passing our models as a list to
the model_selection function and visualising the best
performing metric across different information criteria. Run
?model_selection or see the associated vignette
for more information on customising the plot.
mods = list("ID" = mod_ID, "AV" = mod_AV, "FG" = mod_FG,
"ADD" = mod_ADD, "FULL" = mod_FULL)
model_selection(models = mods, metric = c("AIC", "AICc", "BIC", "BICc"))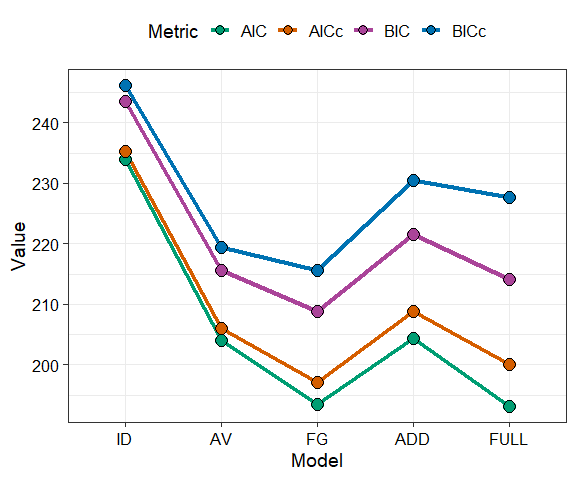
The model mod_FG (labelled as “FG”) is the best model as
it has the lowest value for all the information criteria. We proceed
with this model.
The coefficients are as follows
summary(mod_FG)
#>
#> Call:
#> glm(formula = fmla, family = family, data = data)
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> p1_ID 8.5406 0.7627 11.198 2.50e-14 ***
#> p2_ID 8.7926 0.7627 11.528 9.70e-15 ***
#> p3_ID 16.0825 0.7627 21.086 < 2e-16 ***
#> p4_ID 11.9263 0.7627 15.637 < 2e-16 ***
#> FG_bfg_G_H 17.3817 2.1713 8.005 4.66e-10 ***
#> FG_wfg_G 7.6604 4.4234 1.732 0.0905 .
#> FG_wfg_H 1.0119 4.4234 0.229 0.8201
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for gaussian family taken to be 2.370592)
#>
#> Null deviance: 10290.75 on 50 degrees of freedom
#> Residual deviance: 101.94 on 43 degrees of freedom
#> AIC: 193.51
#>
#> Number of Fisher Scoring iterations: 2After choosing a model we can create diagnostics plot where the
points are replaced by pie-glyphs showing the proportions of the
compositional variables. Run ?model_diagnostics or see the
associated vignette
for more information on customising the plot.
model_diagnostics(model = mod_FG)
#> ✔ Created all plots.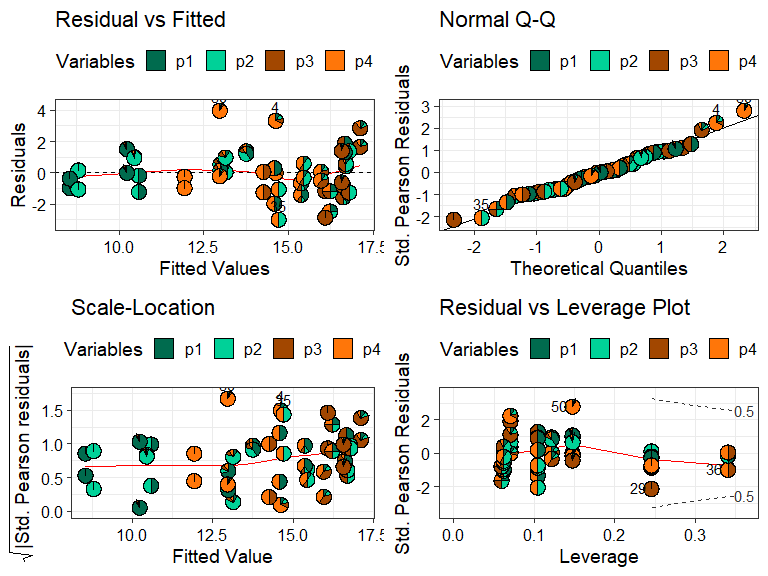
Replacing the points with pie-glyphs could help us to quickly identify any problematic observations in the model. For example, we can see here that the diagnostics plots look fine and no assumptions seem to be violated. However, we can quickly spot that the all monocultures (communities with only 1 species) and certain communities with 2 species have high leverage values compared to all other communities in the data.
We visualise the predicted response for specific observations as a stacked bar-chart showing the contribution (predictor coefficient * predictor value) of each term in the model.
prediction_contributions(model = mod_FG,
data = my_data[c(1:5, 12:15),])
#> ✔ Finished data preparation.
#> ✔ Created plot.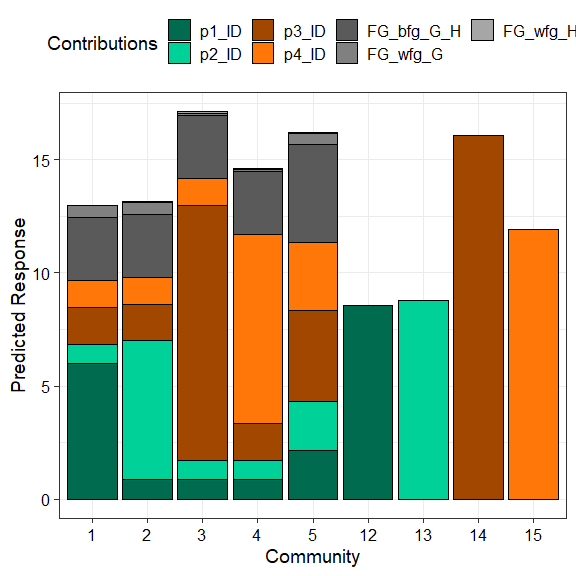
The coloured bars show the contributions of the different terms in the model. The contribution is defined as the product of the coefficient and value for each predictor variable. Thus, the contribution for a term would be zero if it’s value in an observation is zero regardless of it’s coefficient value (e.g. prediction bars for the monocultures at the right of the graph).
This plot would aid in understanding why certain observations have
higher predictions. For example, we can see that higher predictions are
primarily driven by the p3_ID and p4_ID terms
and hence the p1 and p2 monocultures have low
predictions as the all the other terms have a value of zero here.
Similarly, we can also see that mixtures dominated by p3
perform the best. Run ?prediction_contributions or see the
associated vignette
for more information on creating and customising the plot.
Next we show a scatterplot of the predicted response across all equi-proportional mixtures at each level of richness (number of species in a community). The points are replaced with pie-glyphs to show the proportions of the different species while the dashed black line shows the average change in response over the richness gradient.
# Create data including all equi-proportional communities at
# each level of richness
plot_data <- get_equi_comms(nvars = 4, variables = paste0("p", 1:4))
# Show the average change over richness
gradient_change(mod_FG, data = plot_data)
#> ✔ Finished data preparation
#> ✔ Created plot.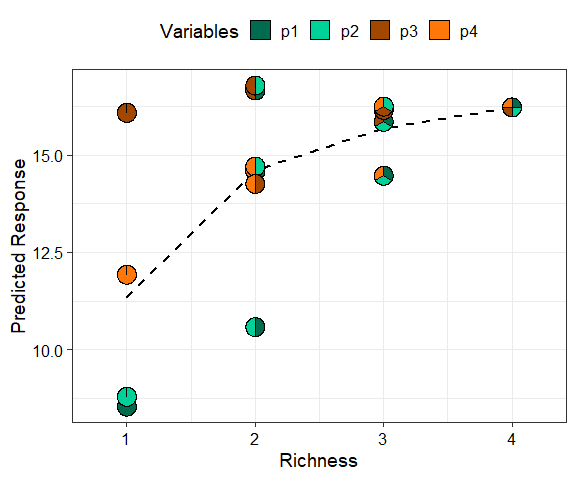
This shows that on average the predicted response increases as
richness increases but at a saturating rate. Run
?gradient_change or see the associated vignette
for more information on creating and customising the plot.
Ternary diagrams are a great tool for visualising the change in a continuous response, however they can only be created for examples with three compositional variables. If we have more than three compositional variables we create conditional ternary diagrams where fix n-3 compositional variables to have specific values and visualise the change in the predicted response across the remaining three variables as a contour plot in a ternary diagram.
For this example, since we have four species we can condition one of
the species (say p2) to have a specific values 0.2, 0.5,
and 0.8 and see how the response is affected as we change the
proportions of the other three species whilst ensuring that the sum of
the four species proportions is 1.
conditional_ternary(model = mod_FG,
tern_vars = c("p1", "p3", "p4"),
conditional = data.frame("p2" = c(0.2, 0.5, 0.8)))
#> ✔ Finished data preparation.
#> ✔ Created plot.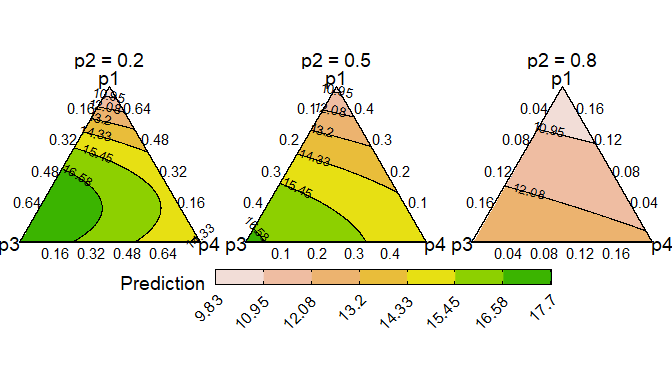
This figure shows that the predicted response decreases as we
increase the proportion of p2 and is maximised as we
increase the proportion of p3. Run
?conditional_ternary or see the associated vignette
for more information on creating and customising the plot.
Effects plots are great for visualising the average effect of a
predictor in a model. However, if the predictors are compositional in
nature, then standard effects plots are not very useful because of the
sum to 1 constraint. The visualise_effects function creates
effects plot for the compositional predictors in a model by ensuring
that the sum to one constraint is respected as we increase or decrease
the proportion of a particular variable.
In this example we specify few communities using the
data argument and see the change in the predicted response
as we increase the proportions of the species p2 and
p3in each community whilst keeping the ratio of the other
species constant.
visualise_effects(model = mod_FG, data = my_data[1:15, ],
var_interest = c("p2", "p3"))
#> ✔ Finished data preparation.
#> ✔ Created plot.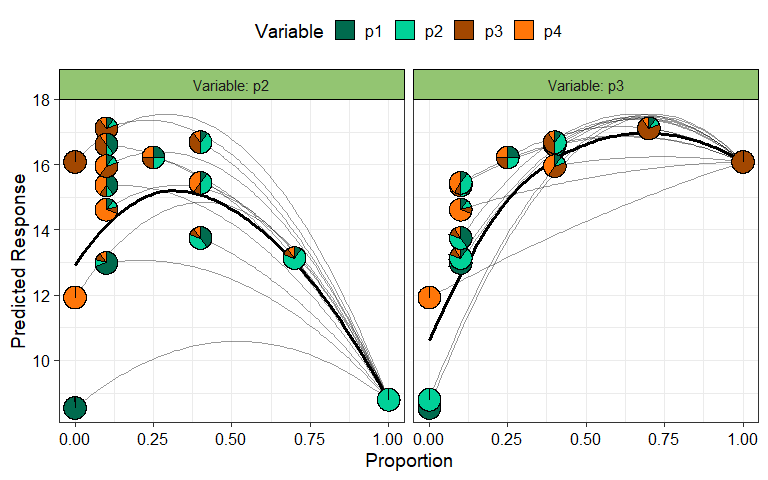
The grey lines show the effect (on the predicted response) of
increasing the species of interest within a particular community while
the solid black line shows the average effect of increasing the
proportion of a species on the predicted response. It can be seen that
for all communities increasing p2 results in a decrease in
the predicted response while increasing p3 has a positive
effect on the predicted response. Run ?visualise_effects or
see the associated vignette
for more information on creating and customising the plot.
The concept used in visualise_effects can be extended to
look at the change in the predicted response as we move in a straight
line between any two points within the simplex space. The interpolation
constant (shown on the X-axis) is a number between 0 and 1 identifying
points along the straight line between the start and end points. We can
even traverse a path comprising of multiple points within the simplex
and see the change in the predicted response. In this example we show
the change in the response as we move from the centroid mixture to the
monoculture of each of the four species.
simplex_path(model = mod_FG,
starts = my_data[5, ],
ends = my_data[12:15, ])
#> ✔ Finished data preparation.
#> ✔ Created plot.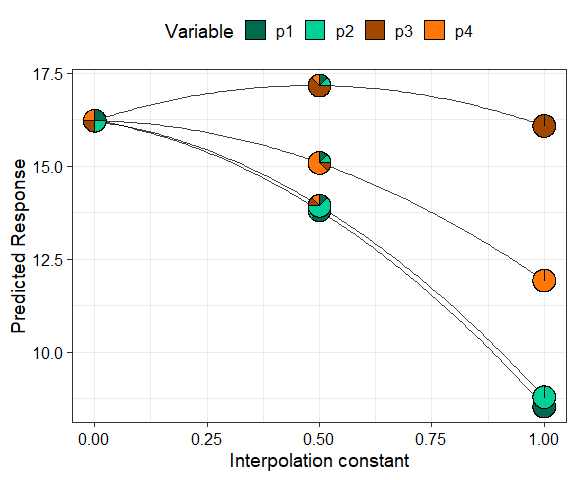
We can see that moving from the centroid community to
p1, p2, and p4 decreases the
predicted response, while moving towards a monoculture of
p3 increases the response. Run ?simplex_path
or see the associated vignette
for more information on creating and customising the plot.